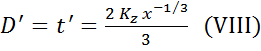SHRINKING MATTER THEORY
1) THE SHRINKING MATTER
THEORY
2) Example
changing to a reference frame in the past
3) The
CMBs and the Shrinking Matter Theory
4) The
Fine-Structure Constant and the Shrinking Matter Theory
5) The redshift
and the time (or distance) relationship
6) The SN1a
distance ladder and the shrinking matter theory
7) Predictions
in the SHRINKING MATTER THEORY
1) THE SHRINKING MATTER THEORY
This theory is not to disprove the big bang theory,
but for those not yet brainwashed by the believers in such theory.
The first step of the Shrinking Matter Theory is a
compact summary, but it contains all the basic mathematic to assume the
universe as the reference frame.
The shrinking matter theory and the expansion universe
theory are equivalent. If we make our world as the reference frame, the
universe should expand. If we make the universe as the reference frame, the
matter should shrink. The laws of physics work to both theories.
The main diference of the expansion universe and the
shrinking matter theory is what is the cause of the longer wavelength observed
of the deep space objects.
The doppler shift (redshift) is well known in the
expansion theory.
In the shrinking matter theory, the universe is the
reference frame, so there is not expansion to cause redshift (except in the
systemic local movements like rotation, orbits, binary systems, turbulence,
ejection, gravitational effect and gravitational falling), so, the longer wavelengths
observed are actually longer emission lines due the bigger size of the atoms in
the past.
If we assume the speed of the light is constant along
the time, the Planck constant “h” should grow by the factor of (1+Z)1/3
in the past. This means the Planck constant decreases along the time.
To simplify, we could call (1+Z)1/3=Kh, so,
h(f)=Kh x h(o).
Z : (observed redshift)
h(f): Planck constant in the observed frame.
h(o): Planck constant of our local frame.
Constant dependence:
We must apply the constant Kh for all formulae and
constants used in physics were the Planck constant “h” is used.
So that simplify the work, we can apply the constant
Kh directly over the used values of our local frame, observing the right
exponential use of the Planck constant as follow;
h(f)=Kh h(o) “Planck constant”
λ(f)=(Kh)³
λ(o) “wavelenght
emission lines”
r(f)=(Kh)² r(o) “Bohr radius”
E(f)= E(o) / (Kh)² “energy of the emission line”
WDC(f)=(Kh) WDC(o)
“Wien Displacement Constant”
R∞(f)=R∞(o) / (Kh)³ “Rydberg constant”
T(f)=T(o) / (Kh)² “Temperature of the emission line
(Wien)”
(f) observed frame in the past.
(o) our local frame at the presente
2)
Example changing to a reference frame in the past
Suppose we search a galaxy and we
detect the Lyα emission being three times greater than the Lyα in our world.
The wavelength is exactly 3647.04 Â.
The H Lyα in our frame is 1215.68 Â.
So, the redshift Z(f) is
Lyα(f)/Lyα(o)-1 = 2
The constant Kh is (1+Z(f))1/3
= (1+2)1/3 =1.44224957
So, Kh=1.44224957
Now we can determine the main
constants of the reference frame in the past;
cst/vle formula* local frame(o) past frame(f)
h(f) h(o) (Kh) 6.62606957E-34 Js 9.5564460E-34 Js
Lyα(f) Lyα(o)
(Kh)³ 1215.68 Â 3647.04 Â
r(f) “Bohr” r(o)
(Kh)² 0.529 Â 1.1007 Â
E(f) E(o) / (Kh)²
10.204 Ev 4.906
Ev
WDC(f) WDC(o) x (Kh) 0.0028978 mK 0.0041796 mK
R∞(f) R∞(o) / (Kh)³ 10973730.68 m-¹ 3657910.22 m-¹
T(f) T(o) / (Kh)² 23836 ºK 11459 °K
(f) observed frame in the past
(o) local frame at the present
* simplified formula
If we consider Ho=71 km/s/mpc and
assume it is enough to determine the distance, we have:
distance= 3380.3 mpc = 11.02 Gly
time (past) = 11.02 Gyr
Ho= Hubble constant
3) The CMBs and the Shrinking Matter Theory
The lack of peak
bandwidth emissions pattern avoids us to determine exactly what actually the
CMBs are. This could let us to various scenarios.
3.1) One is
assuming the CMBs could be the first thermal emission lines. In this scenario,
if we consider the CMBs are Lyman alpha emissions, we have:
Temperature:
______________56.15 K
Wavelength:
______________1.063214 mm
Energy:
__________________0.024039 eV
WDC
:____________________0.059703 mK
Z:
_______________________8744.81
3.2) An other
scenario is assuming the CMBs could be hydrogen fine structure emission lines.
In this case, the redshift is negative (blue shift), and the radiation could be
the remaining of the collapsed universe, which provided the energy to the
emergence of the universe we know. In this case we have:
Temperature:_____________0.46721 K
Wavelength:
______________1.063214 mm
Energy:
__________________2 (10)-4 eV
WDC:__________________4.967462
(10)-4 mK
Z (blue
shift):_____________-0.99496253
The
shrinking matter theory states that the Planck constant “h” varies along the
time, so the energy of the emissions also varies with the time. In this
scenario, there is a systematic error in our researches assuming that the
observed waves, emitted in the past and detected in our devices have the same
energy as the waves produced in our local frame. We shouldn’t forget that the
waves with the same frequency can be added and give the impression that they
are more energetic. The amount of energy of each wave could be determined by
the receptor, but it may not represent the real emitted energy of the wave.
The peak of
the CMBs are the most populous microwaves in the universe, as well the hydrogen
is the most abundant element in nature, so, for now we should suppose (and
state), the CMBs are the hydrogen fine structure emission lines of the
collapsed universe which provided the energy to the emergence of the universe
we know. I know it is a hard exercise for the minds which are indoctrinated in assuming
the BB as a fact, but I hope you can. We know the CMBs are the most distant
emissions detected, among the unresolved CXRBs, so, in this scenario, the
wavelength of the CMB, compared with the hydrogen fine structure emission in
our reference frame (21 cm), result a negative redshift (blue shift), this could
only be attributed to the remaining fine structure emissions of the hydrogen in
its collapsed last phase of the cyclic universe.
In this
scenario, as issued later, the redshift is negative (blue shift), and can be
calculated as follow:
Z = -0.99496253
Kh = (1+Z)1/3
= ( 1 – 0.99496253)1/3 =>
Kh = 0.171
423 684
The Planck
constant h(f) in this scenario would be:
h(f) = Kh x h(o) =>
h (f) = (0.171
423 684) ( 6.626 069 57) (10)-34 =>
h (f) = 1.135
865 258 (10)-34 Js
When we
replace the h(o) by the h(f) in the formulae, we have:
r(f) = 1.555
pm (Bohr radius)
Lyα(f) = 6.123975
Â
E (Lyα(f))
=347.248 eV
E (n=1) =
-463 eV
T (Lyα(f))=
811 150.06 K
WDC = 4.967462
(10)-4 mK
In this
transition, (Lyα(f)), the fine structure emission lines can happen in the
ground state and would be:
Temperature:_______________0.46721 K
Wavelength:_______________1.063214
mm
Energy:___________________2.00
(10)-4 eV
WDC:____________________4.967462
(10)-4 mK
The unexpected
and most important result in this scenario is that the Lyα(f) falls surprisingly
in the lower end band of the unresolved CXRB (Cosmic X-Ray Background). So, the
shrinking matter theory (in this scenario) could solve the origin of the CMB
and the unresolved CXRB as being remnants of the past collapsed universe, and
the future of this universe. Of course this needs further resources, but it is a
strong evidence of the consistence of this theory.
4) The Fine-Structure Constant
and the Shrinking Matter Theory
The fine-structure
constant “α” is a dimensionless value, but it reflects the relationship between
the electromagnetic coupling constant ‘e” and ”Ԑₒ”, “h”, and “c”.
e = (2 α Ԑₒ
h c)1/2 or e² = 2 α Ԑₒ h c
As c is
constant, result Ԑₒ is also constant, then α should vary with the inverse of
the rate of h.
Rewriting
the expression we have:
α = e² / (2
Ԑₒ c h), and
α(o) = e² /
(2 Ԑₒ c h(o) ) =>
α(f) = e² /
(2 Ԑₒ c h(f) ) =>
α(f) = e² /
(2 Ԑₒ c h(o) (Kh))
Then α(f) =
α(o) / Kh
Or α(f) = α(o)
/ (1+Z)1/3
α(o) = 0.007
297 352 5698(24)
(o): our
local frame
(f): distant
reference frame
Z : redshift
Kh: scaling
factor of the Planck constant h as a function of Z
“However, if multiple coupling constants
are allowed to vary simultaneously, not just α, then in fact almost
all combinations of values support a form of stellar fusion.” https://en.wikipedia.org/wiki/Fine-structure_constant
5) The redshift and the time (or
distance) relationship
Since in the
Shrinking Matter Theory there is not receding speed, there is no reason to
determine the distance based in the standard model (expanding universe), which
is necessary determine the apparent receding speed to infer the distance based in
the Hubble constant.
In the
Shrinking Matter Theory, the size of the atom decrease along the time, so the
time should be defined by the rule of lost in volume per unit of time (LVL).
The LVL can be mathematically defined as dVL /dt.. The
LVL should vary along the time, according to the size of the atoms, and this
variance could be proportional to the surface or to the volume of the atoms
along the time.
This would
let us to two hypotheses, A, and B.
The
hypothesis A proposes the LVL variance could be proportional to the surface of
the atoms.
The
hypothesis B proposes the LVL variance could be proportional to the volume of
the atoms.
Now we can
develop the two hypotheses to analyze the possibility of choose the one which
best fit to the observations.
5.1)
Hypothesis A:
This
hypothesis proposes the LVL (dVL/dt) varies proportionally to the
surface Sf of the atom, so we can write:
The volume
of the atom VL can be defined by the
function:
We can call x = (1+Z), so,
Sf = 4 π rf
2 =>
Sf = 4 π (ro
(1+Z)2/3)2 =>
Sf = 4 π ro2
(1+Z) 4/3 =>
Replacing
(1+Z) by x, we have:
Sf = 4 π ro2 x4/3 (III)
Applying (II) and (III) in (I), we have
ro
x2/3
= rf , so, the time is directly proportional to the radius of the atoms. This
case is similar to a spherical block of ice defrosting in an isothermal medium.
The release of liquid water decreases along the time, because it is
proportional to the surface of the block, but the decreasing in the diameter is
constant per unit of time.
but, ro / Ks is constant and we can replace it by Kz, so,
For Z = 0 => x=1 and t = 0
So, for Z = 0 we have:
0 = Kz
(1)2/3 + C =>
C = -Kz =>
We usually
use the time in Gyr (giga years) or Myr (mega years)for astronomical units,
because it can be directly converted in distance Gly (giga light years) or Mly
(mega light years).
So, we can
say:
D = t = Kz (1(x2/3- 1) (IV)
x = (1+Z)
D = Distance
(Gly)
t = Time
(Gyr)
Kz = Stretching factor of the function so that fitting
it to the measured observations at low redshifts.
The redshift
Z can now be expressed in function of
the time t as follow:
x = (1+Z) =>
t : (Gyr)
The farthest
bodies newly observed present redshift of about Z =8, so we should limit our researches in in the range of Z from 0 to 8
The distance
D in the standard model for Z= 8 is
13.436113 Gly,
The Bohr
radius in the shrinking model ro and
rf are:
ro = 5,291773 x 10-11 m
(for Z=0)
rf
= 2,899617 x 10-10 m (for Z=8)
ro = Bohr radius of the hydrogen in the ground
state at the present, in our local frame (m).
rf = Bohr radius of the hydrogen in the ground
state in the past frame (m).
For the
hypothesis A, the above equation (IV), is the basic to define all the
relationships in the Shrinking Matter Theory.
Now we can
determine the best value for the constant Kz,
so that calibrating the equation to the observed distances. This
calibration must be done at low redshift, where we can determine the distances
by parallax. This mean the above function should give us the same value when
the redshift is null (zero), and at low redshifts give us neglected
differences. This mean the tangent of the above function (IV), at Z= 0, should have the same as the
tangent in function of the standard model (expansion universe).
In the
standard model, (expanding universe), the equation to define the distance can
be expressed as follow:
c = light speed = 299792458 m/s
H0 = Hubble constant = 71 km/s/mpc
To take the
result in Gly, the equation becomes:
We can
replace (1+Z) by x, then,
x2 -
1 = u
x2+1 = v
The function
to determine the distance in the shrinking model is:
D = t = Kz ( x2/3-1) (IV) =>
x = (1+Z)
For Z = 0,
=> x = 1
To force the
tangency of the two functions (IV) and (VI) at x = 1, implies (VII) = (VIII) at x=1, so, matching (VII) and (VIII), we have:
Kz = 20.65802330515155 (best value for Kz, for hypothesis
A, for Ho = 71)
c = light
speed = 299792458 m/s
H0 = Hubble constant = 71 km/s/mpc
5.1.1) Shrinking speed SHV along the time in function of the
redshift
The
shrinking speed SHV of the Bohr
radius can be defined as dr/dt.
The Bohr
radius in the past is defined by the function:
SHV
= 8.117414 (10)-29 m/s
= constant (for hypothesis A)
The
Shrinking speed is constant along the time.
5.1.2) Specific
shrinking speed (SPV)
The specific
shrinking speed is defined as Vf
/ rf .
Vf : Shrinking speed in a reference frame SHV (IX).
rf : Bohr
radius in a reference frame. rf (VIII).
x=1+Z
For Z = 0
=> x = 1
=> SPV = 1.534 (10)-18
m/s /m
The equatorial
radius of the Earth is 6 378 136.3 m.
The
shrinking speed of the Earth would be:
SHV =
(6378136,3) (1.534) (10)-18
=>
SHV = 9.7839
(10)-12 m/s
1 year = 31 556 926.08 seconds, so,
SHV = (31 556 926.08) (9.7839)(10)-12 m/year
=>
SHV = 3.0875
(10) -4 m / yr
SHV =
0.30875 mm / yr
SHV =
308.75 m / Myr
5.2) Hypothesis B:
This
hypothesis proposes the LVL (dVL/dt)
variance is proportional to the volume VLf of the atom, so we can write:
The volume
of the atom VL can be defined by the function:
rf
= ro (1+Z)2/3 =>
But, 2/Kv is constant, so, we can call 2/Kv = Kz, then:
For Z = 0 => x=1
and t = 0
So, for Z=0,
we have:
t = Kz ln (x) (XIII )
e = 2.718 281 828 459 05
t : (Gyr)
KZ =
Now we can
determine the best value to the constant Kz,
so that calibrating the equation to the observed distances. This
calibration must be done at low redshift, where we can determine the distances
by parallax. This mean the above function should give us the same value when
the redshift is null (zero), and at low redshifts give us neglected
differences.
This mean
the tangent of the above function at Z=
0, should be the same as the tangent in the respective function of the standard
model (expansion universe).
In the
standard model, (expanding universe), the equation to define the distance can
be expressed as follow:
x = (1+Z)
For Z = 0,
=> x = 1
To force the
same tangency in the two functions (XIII) and (VI) at x = 1, implies (XII) = (VII) at x=1,
so, matching (XII) and (VII), we have:
c = light speed = 299792458 m/s
H0 = Hubble
constant = 71 km/s/mpc
KZ = 13.772 015 536 767 7 (best value for Kz in the function (XIII), hypothesis B, for Ho = 71)
5.2.1) The Shrinking speed SHV along the time in function of the
redshift
The
shrinking speed SHV of the Bohr
radius can be defined as dr/dt.
The Bohr
radius in the past is defined by the function:
rf = ro
x2/3 =>
t = Kz ln (x) (XIII
) =>
x = (1+Z)
5.2.2) Specific shrinking speed (SPV)
The specific
shrinking speed SPV is defined as Vf
/ rf .
Vf : Shrinking speed in a reference frame SHV (XIV).
rf : Bohr radius in a reference frame.
rf = ro x2/3
=>
SPV = 1,5339
(10)-18 m/s /m
SPV =
47.333 km/s /mpc
5.2.3) The Shrinking acceleration
(SHA) along the time in function of the redshift
The
shrinking acceleration SHA is defined
as the variation of the speed in function of the time, so, it can be defined
mathematically as:
V = SHV (XIV) and
dt = (XII)
x = (1+Z)
x = (1+Z)
5.2.4) Specific shrinking
acceleration (SPA) along the time in function of the redshift
The specific acceleration SPA
is defined as the shrinking acceleration SHA
per unit of length.
This means as bigger the length of a body, as bigger the SHA.
The SPA
can be defined as:
SHA: (XVI) and rf = ro
x2/3
For hypothesis B, SPA = Constant = 7.4245 (10)-23 m/s /m /Myr
For hypothesis B, SPA = Constant = 2.2909 (10)-3 km/s
/mpc /Myr
The Graphic 01 presents the comparative evolution of the distance (Gly)
or time (Gyr), for the shrinking Model hypothesis A “Time shrM A”, the
shrinking Model hypothesis B “Time shrM B”, and the standard Model “Time stdM”.
Graphic
01
6) The SN1a distance ladder and the
shrinking matter theory
The Shrinking
Matter Theory is characterized by the possibility of vary the Planck constant
along the time as the factor of the redshift of the emissions in the past.
This
justifies the bigger size of the atoms and bodies in the past, as well the
longer wavelength emissions and smaller energy and temperature.
The main
relationship relative to the proprieties of the matter and the redshift is
listed below.
hf =
ho (1+Z)1/3 Planck constant
λf = λo (1+Z) wavelength
emissions
rf = ro (1+Z)2/3 Bohr radius,
energetic n level radius, and bodies size.
Ef
= Eo (1+Z) -2/3 Energy of the line
emissions.
WDCf
= WDCo (1+Z)1/3 Wien Displacement Constant
R∞f
= R∞o(1+Z) -1 Rydberg constant
Tf
= To (1+Z)-2/3 Temperature of the line
emissions
The SN1a
distance ladder is a system used to calculate the distances based in the
hypothesis which their luminosity peak is constant, so, as fainter the flux
received in our telescopies, as longer the distance from the Earth. The
relationship between the distances and the flux is:
F1
and D1 are flux an distance of a near and known SN1a, which distance
can be determined by parallax, used as standard reference.
F2 is
the measured flux of a more distant SN1a, and D2 is the unknown
distance to be calculated.
The absolute
magnitude μ is a logarithm scale where:
But,
The adopted
standard distance D1 ‘is
10 pc, so that simplify the equation, since log10 = 1. The equation so becomes:
μ = 5 logD2 – 5 (D2
: pc) (XX)
This
equation works well for low redshifts, but in the Shrinking Matter Theory the
flux F2 is affected by the redshift. In the past the energy of the
emissions was smaller, and such energies were spread onto a bigger
surface.
The energy
of the emissions in the past is defined by the function Ef
= Eo (1+Z) -2/3, and the surface by the function Sf
= 4 π rf 2.
To nullify
the effects of the redshift in flux F2,
we should replace it by corrected flux F2c .
The F2c is defined by the
function:
F2c = F2 (1+Z)2 (XXI)
Then, the
relationship between the fluxes and the distances becomes:
The absolute
magnitude function for the Shrinking Matter Theory becomes:
μ = 5 (logD2
+ log(1+Z) – logD1)
D1 = 10 pc => logD1
= 1 =>
μ = 5logD2
+ 5log(1+Z) – 5 (XXIII)
D2 :( pc )
The graphic
02 presents the comparative evolution of the absolute magnitude μ.
The
evolution of the expected μ to the Shrinking Matter Theory, hypothesis A is in
red color.
The
evolution of the expected μ to the Shrinking Matter Theory, hypothesis B is in
green color.
The
evolution of the expected μ to the Standard Model (expanding universe) is in
black color.
The observed
evolution of the absolute magnitude μ is represented by square blue points,
which were extracted from Betoule et al 2014, Table F1, page 30, “http://arxiv.org/pdf/1401.4064v2.pdf
“.
Graphic 02
The curve
which best fit to the observational data is the hypothesis A of the Shrinking
Matter Theory “shrM A abs mag”. No need for dark energy.
7) Predictions in the
SHRINKING MATTER THEORY
7.1) The Effects of the
shrinking matter in the local frame
The
expansion universe considers that the local frame is not affected by the
expansion due the gravitational bond of the bodies. This statement is
contradictory because the limit of the gravitational bond is very difficult to
define, maybe there is not such limit.
In the
shrinking matter theory the shrinking effect happens everywhere, so the orbit
of the Earth and the planets should present an apparent growing along the time.
The distance
between the Earth and the Sun is very difficult to determine precisely. The
apparent expansion should be about 7.26 m/year. For ones this could be a great
variation, for others small. The true is that we cannot use a stick to measure
it. The fact is that such distance varies every time, since the orbit is
elliptical, but the eccentricity of the orbit also varies due the tide effect
of the planets of the solar system. Here we have a great challenge to measuring
this distance with enough accuracy to detect this variance.
The only way
to measure it precisely should be launching two space craft’s, similar to the
JWST, positioned in the L4 and L5 Sun-Earth Lagrangian points. If we measure
precisely the distances between these two points whole the year, we could
determine the average distance.
7.2) The remaining
emissions from the last collapsed universe
In the third
chapter we have two possible scenarios concerning to the origin of the CMBs.
If we adopt
the second scenario (3.2), we can make an interesting prediction.
When we can
get more accurate measurements of CXRBs, probably, we can distinguish two peaks
at the end of the lower energetic band. These peaks should be 2025.67 eV and
2400.80 eV detected in our devices, corresponding to the Lyα and Lyβ emissions respectively.
When
corrected by the appropriated Planck constant of the reference frame, the
energies and the wavelength of these emissions should be:
Lyα: E = 347.25 eV λ = 6.1240 Â
Lyβ E = 411.55 eV λ = 5.1671 Â